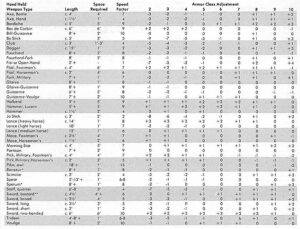
AD&D’s weapon versus AC adjustment table is the online recipe of tabletop RPGs. Everybody that talks about it wants to talk around it. Or talk about their houserules. Or talk about people talking about it. Or talk about how they calculated them better than Gary. Or sell you on shortcuts. Nobody ever just explains it.
So let’s do that today.
Why is simple – some weapons are better against some armors than others. This is the fun of the trade-offs of RPGs. It’s the rock-paper-scissors game write large in man-to-man combat. It opens up a host of tactics and helps to supercharge those long-belittled first level fighters who now have ways to impact the enemy beyond “which one does the most damage?”
When to do it can be a judgement call. Gary explicitly says this is for armor, but that you can use this system for animal hide (treat as leather or maybe plate) if you want to. For the most part, this subsystem is most useful for bipeds in protective wrapping beating on each other. That should become more clear as we go.
How to do it isn’t very hard, except that you have to stop thinking of AC as a pure number and think of AC as an armor type instead. Thanks to DEX bonuses, magic items, and situational modifiers you can land on any particular AC score in a lot of ways. But for this step of calculating a to-hit number, just think of the target first as a guy in a kind of armor. Forget DEX and that ring of protection +1, we’ll roll those in later. Right now, we’re just looking for that basic to-hit number.
So first find the AC adjustment, and that means turn to Table 50 from the Players’ Handbook.
All you do is adjust the AC of the target by the amount shown. Those are pure adjustments. A voulge striking at a guy in plate+shield treats that AC2 as a an AC1 target. A two handed sword swinging at the same guy treats him as having an AC4.
Okay, now you can start slapping on dexterity modifiers and magic rings and such to find the final target AC. Apply your striking bonuses and penalties from strength or dexterity or magic conditions such as bless to the AC as well and you can finally cross-reference the Attack Matrix. Check the chart below, roll them bones, and if you get the number you get to reach for the damage dice.
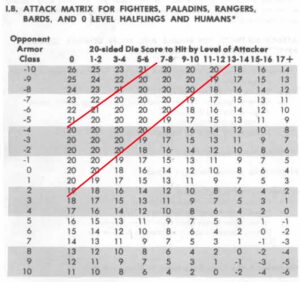
That’s it. You’re done.
Now let’s circle back around to some deeper analysis. Specifically, why do we apply modifiers to the target AC and not to the die roll?
Gary explains the rationale a couple pages (pg 70) before the Attack Matrices:
Certain spells such as curse, prayer, and protection from evil adjust the chance “to hit” of either the attacker or the defender or both. Such changes MUST be made to the armor class of the figure concerned, not to the dice score rolled in attacking. An inspection of the combat tables will show that the dice roll progression will make some opponents hit proof if the dice rolls are adjusted downwards rather than the armor class being moved upwards.
You see those red lines partitioning off the Zone of Natural 20s in the Attack Matrix above? Let’s look at that a little closer, and let’s compare what the to-hit progression looks like in AD&D versus 3e and its descendants.
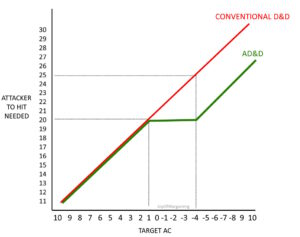
Gary gives us a little plateau there right at the Natural 20 point. It’s six steps long, or five extra steps if you want to think of it that way, and each step doesn’t change the die roll needed to-hit.
It’s worth noting that in most cases applying modifiers to the die roll is the same thing as applying modifiers to the AC. However, given the odd little edge cases lurking in the shadows, you’re better off just calculating the to-hit number the same way every time. That way you won’t miss out on the edge cases.
Here’s an example of when one of those edge cases comes into play. Let’s say you’ve got two 1st level fighters going up against each other. They are both in plate+shield and have a DEX bonus to AC that gives them a final AC1. One of those fighters gets hammered by a curse spell. They are both only hitting on Natural 20s. Let’s say one of our heavy fighty boys gets hit by a curse spell. There are two ways to approach the situation:
- Adjust his opponent’s AC to AC0 which has no effect on the to-hit probability. It is still a 20 to hit.
- Adjust his die roll by -1 which makes rolling a 20 impossible. Even a Nat20 is only a 19, and the fight is over.
Gary explicitly says to use the former.
Admittedly, with enough penalties our beleaguered fighter (cursed, blinded , and on slippery ground) might wind up with an impossible task. He would be swinging at an effective AC-5 for which he needs to roll a 21 on a d20. It happens, but it takes a lot more effort to get him there. Unlike modern iterations of the game which allow for impossible shots at AC21…but then preclude the possibility of impossible shots by allowing success on any Nat20. The second-order effects of this little shift from step-loss to linear progression are subtle, yet profound. There is a point of diminishing returns in Gary’s game that modern iterations lack. There is a point at which the impossible can be achieved in Gary’s game that modern iterations lack. The incentive structures change in real and dramatic ways that few modern players appreciate and even fewer modern designers even understand.
Anyway, the point here is that the weapon versus AC chart is pretty easy once you get your head around it.
It’s certainly a lot easier to use than it is to deduce from the rules, and apparently it’s a lot easier to analyze and think about than it is to explain. At least if the blogosphere results are anything to go by.
Not everybody though. Here is some additional reading from sources I trust:
- Castleport, who also pointed out to me tha “for the weapon vs AC table at least; positives can be considered pluses to hit, since there is no equivalent to the “5 steps” before you can’t hit anymore”
[Editor’s note: I reserve the right to amend this as the peanut gallery weighs in and offers corrections and clarifications. I’ll keep a record of changes here.]